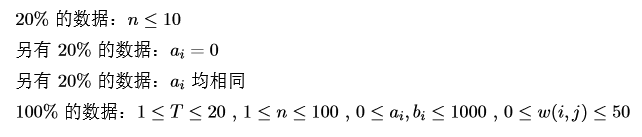String Problem

Time Limit: 10 Sec Memory Limit: 64 MB

Description

img

Input

img

Output

img

Sample Input

1
　　3
　　135
　　1 2
　　1 2
　　1 2
　　1 2
　　1 2
　　1 2
　　1 2
　　1 2
　　1 2
　　1 2
　　0 0 3
　　1 0 0
　　4 0 0

Sample Output

3

HINT

img

Solution

官方题解：

首先将点分为3类

第一类：Pij 表示第i个点和第j个点组合的点，那么Pij的权值等于w[i][j]+w[j][i]（表示得到的价值）

第二类：原串中的n个点每个点拆出一个点，第i个点权值为 –a[s[i]] （表示需要的花费）

**第三类：**对于10种字符拆出10个点，每个点的权值为 -(b[x]-a[x])

那么我们可以得到一个关系图 ，对于第一类中的点Pij，如果想要选择Pij，你就必须要选中第二类中的点i和j，对于第二类中的点如果你想选中第i个点，其对应的字符s[i]，那么就必须选中第三类中s[i] 对应的点，因为每个种类的点第一次选中时花费是b[s[i]]，而第二类中花费都是a[s[i]],一定要补上b[s[i]]-a[s[i]]，而且只需要补上一次。

得到上面的关系图后然后就是普通的最大权闭合子图问题,直接求解即可。

然后我们得到了若干关系，直接建边跑一边网络流即可。

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
#include<bits/stdc++.h>
using namespace std;

const int ONE = 200005;
const int POI = 6005;
const int INF = 2147483640;

int Q,n;
int S,T;
char s[105];
int Val[105][105];
int next[ONE],first[POI],go[ONE],w[ONE],tot;
int Dep[POI],q[ONE],E[POI],tou,wei;
int part1,part2,part3;
int Ans;

struct power
{
    int a,b;
}a[15];

int get()
{
    int res=1,Q=1;  char c;
    while( (c=getchar())<48 || c>57)
        if(c=='-')Q=-1;
    if(Q) res=c-48;
    while((c=getchar())>=48 && c<=57)
        res=res*10+c-48;
    return res*Q;
}

void Add(int u,int v,int z)
{
    next[++tot]=first[u];   first[u]=tot;   go[tot]=v;  w[tot]=z;
    next[++tot]=first[v];   first[v]=tot;   go[tot]=u;  w[tot]=0;
}

int Bfs()
{
    memset(Dep,0,sizeof(Dep));
    tou=0;  wei=1;
    q[1]=S; Dep[S]=1;
    for(int i=S;i<=T;i++) E[i]=first[i];
    while(tou<wei)
    {
        int u=q[++tou];
        for(int e=first[u];e;e=next[e])
        {
            int v=go[e];
            if(Dep[v] || !w[e]) continue;
            Dep[v]=Dep[u]+1;
            q[++wei]=v;
        }
    }
    return (Dep[T]>0);
}

int Dfs(int u,int Limit)
{
    if(u==T || !Limit) return Limit;
    int from=0,f;
    for(int &e=E[u];e;e=next[e])
    {
        int v=go[e];
        if(Dep[v]!=Dep[u]+1 || !w[e]) continue;
        f=Dfs(v,min(Limit,w[e]));
        w[e]-=f;
        w[((e-1)^1)+1]+=f;
        Limit-=f;
        from+=f;
        if(!Limit) break;
    }
    return from;
}

void Solve()
{
    Ans = tot = 0;
    memset(first,0,sizeof(first));
    n=get();
    scanf("%s",s+1);
    for(int i=0;i<10;i++)
        a[i].a=get(), a[i].b=get();
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            Val[i][j]=get();

    part1 = n*(n-1)/2;    part2 = n;    part3 = 10;
    S=0;    T= part1 + part2 + part3 +1;
    int num = 0;
    for(int i=1;i<=n;i++)
        for(int j=i+1;j<=n;j++)
        {
            num ++;    Ans += Val[i][j]+Val[j][i];
            Add(S,num, Val[i][j]+Val[j][i]);
            Add(num,part1+i, INF);
            Add(num,part1+j, INF);
        }

    for(int i=1;i<=n;i++)
    {
        Add(part1+i,T, a[s[i]-'0'].a);
        Add(part1+i,part1+part2+s[i]-'0'+1, INF);
    }

    for(int i=0;i<10;i++)
        Add(part1+part2+i+1,T, a[i].b-a[i].a);

    while(Bfs()) Ans-=Dfs(S,INF);

    printf("%d\n",Ans);
}

int main()
{
    Q=get();
    while(Q--)
        Solve();
}